浮世随记

时间、空间复杂度

说明： 书面说法看书，笔记记理解

提示

一般，T()表示时间复杂度，O()表示趋势函数。这里就不细分，统一用T()了。

时间复杂度分析

  1. 常量阶

    T(1)

    int i = 8; 
int j = 6; 
int sum = i + j;

  2. 平方阶 —— 看多少个循环

    一个循环T(n)

    int cal(int n) { 
  int sum = 0; 
  int i = 1; 
  for (; i <= n; ++i) { 
    sum = sum + i; 
  } 
  return sum; 
}

    两个循环T(n^2)

    int cal(int n) {
  int sum = 0;
  int i = 1;
  int j = 1;
  for (; i <= n; ++i) {
    j = 1;
    for (; j <= n; ++j) {
      sum = sum +  i * j;
    }
  }
}

  3. 对数阶 —— 关注下标是否跳跃

    下标跳跃 T(logn)

    i=1;
while (i <= n) {
  i = i * 2; 
}

    提示

    下标不跳跃： 1,2,3,4,5,...
    下表跳跃： 1,2,22,22*2,...

  4. 线性对数阶 —— 上面两种情况的集合

    T(n*logn)

    for n
  i=1;
  while (i <= n) {
    i = i * 2; 
  }

还有 指数阶T(2^n)、阶乘阶T(n!) 基本不会遇到。
下面是不同时间复杂度的性能发展：

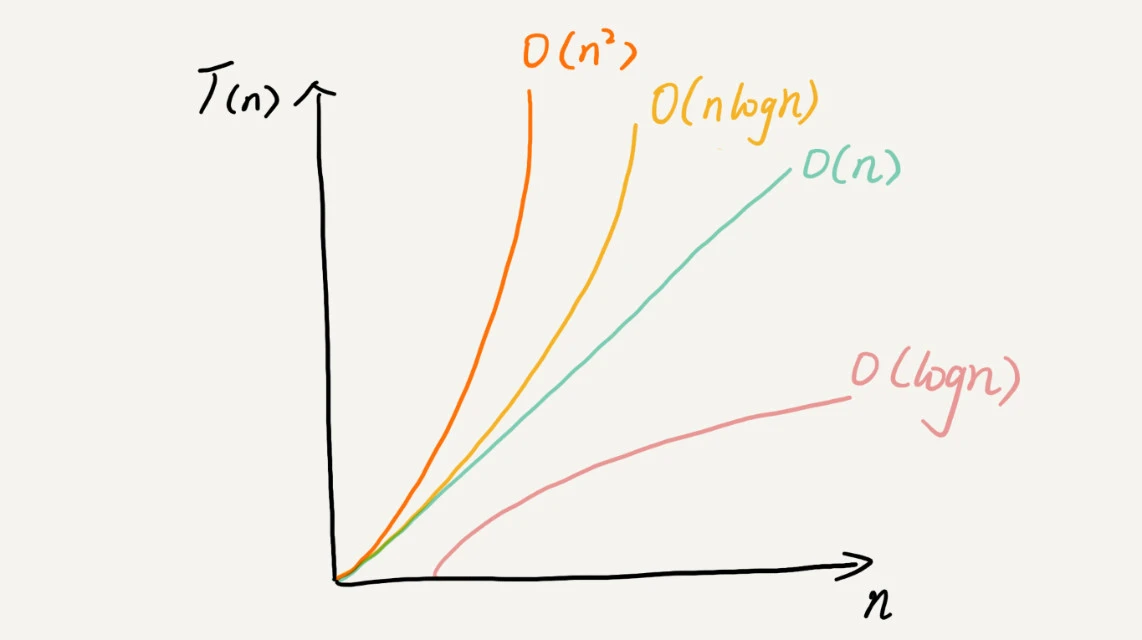
497a3f120b7debee07dc0d03984faf04.webp

空间复杂度分析

表示生成了多少个内存变量。

常见的 O(1)、O(n)、O(n^2)

如： 下面是 O(n)

void print(int n) {
  int i = 0;
  int[] a = new int[n];
  for (i; i <n; ++i) {
    a[i] = i * i;
  }

  for (i = n-1; i >= 0; --i) {
    print out a[i]
  }
}

细分时间复杂度

  • 最好情况时间复杂度（best case time complexity）
  • 最坏情况时间复杂度（worst case time complexity）
  • 平均情况时间复杂度（average case time complexity）
  • 均摊时间复杂度（amortized time complexity） —— 特殊的“平均情况时间复杂度” —— 用“摊还分析法”分析，将最坏情况时间均摊到其他情况中，往往统计结果得到最好时间情况。

数据结构和算法

20 个重点： （按常用程度/难易程度排序）

数据结构 - 数组

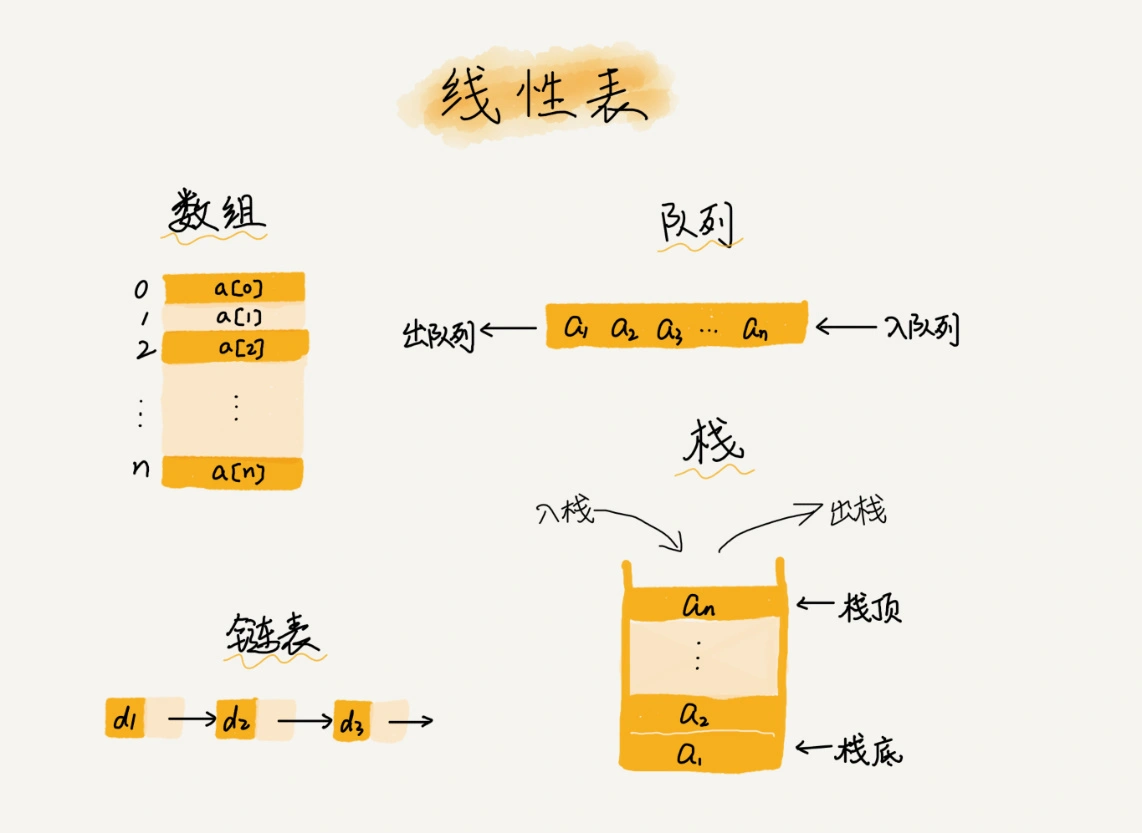
b6b71ec46935130dff5c4b62cf273477.webp

数组类型

  1. 有序数组
  2. 无序数组 —— 单纯用来存数据

数组应用

  1. 添加时需要遍历 —— 无序数组插入时可用快排优化添加情况：将插入的位置原数据放最后，插入的新数据放空坑；
  2. 删除时需要遍历 —— 标记删除优化删除情况，如 JVM 的标记删除垃圾回收机制

数据结构 - 链表

链表类型

  1. 单向链表

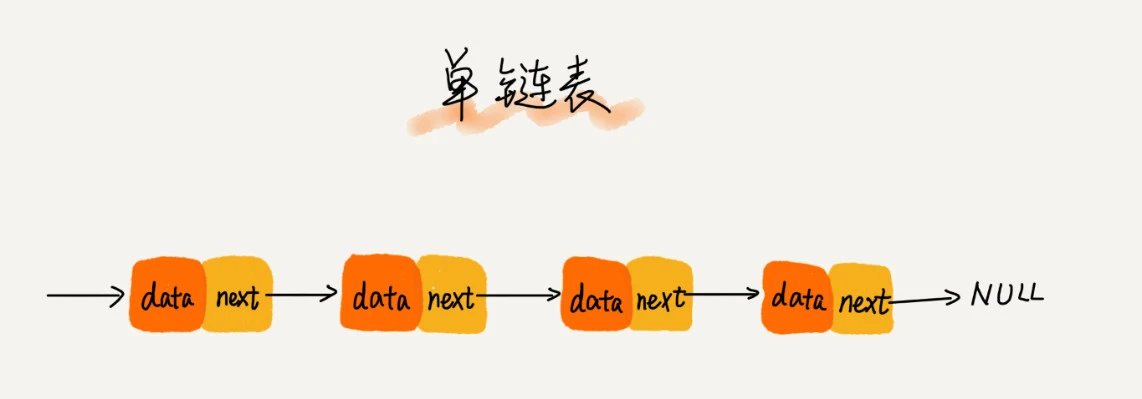
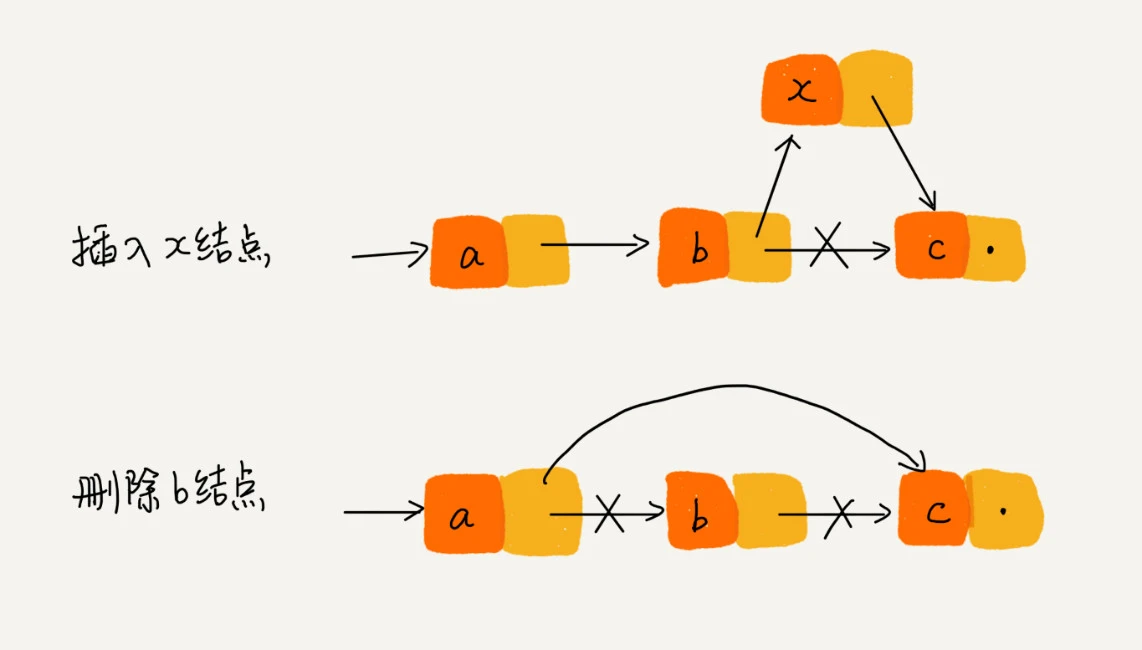
    b93e7ade9bb927baad1348d9a806ddeb.webp452e943788bdeea462d364389bd08a17.webp

  2. 循环链表

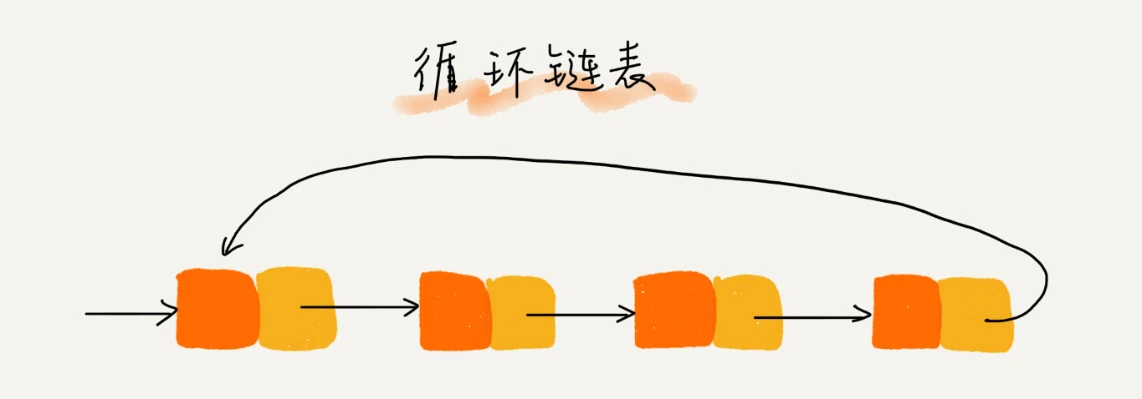
    86cb7dc331ea958b0a108b911f38d155.webp

    约瑟夫问题 https://zh.wikipedia.org/wiki/约瑟夫斯问题在新窗口打开

  3. 双向链表

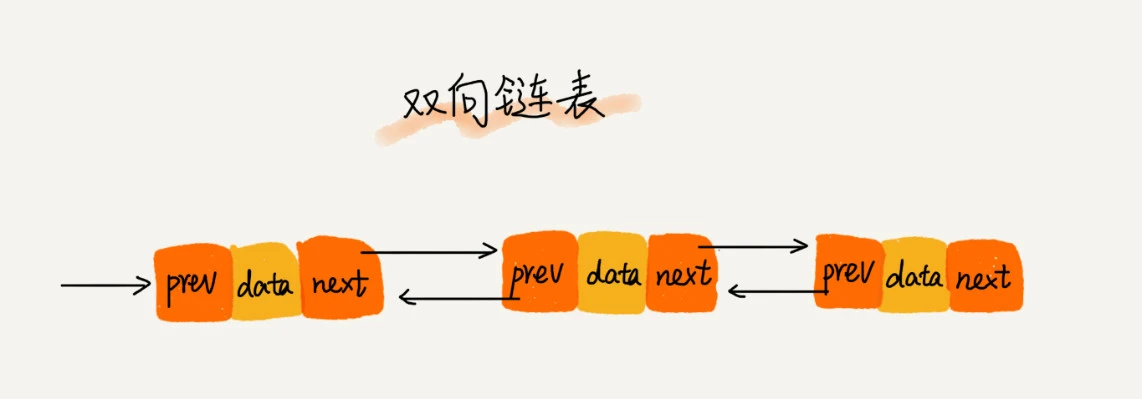
    cbc8ab20276e2f9312030c313a9ef70b.webp

链表应用

  1. LRU 缓存淘汰算法 —— 维护一个有序单链表。当有数据被访问，遍历链表删除相同数据并在头部插入数据。当有缓存要清除，删除尾部数据。 时间复杂度O(n)

    提示

    缓存清理通常有三种策略： 先进先出策略 FIFO（First In，First Out）、最少使用策略 LFU（Least Frequently Used）、最近最少使用策略 LRU（Least Recently Used）

链表题目

  1. 如何判断一个字符串是否是回文字符串的问题

    使用快慢两个指针找到链表中点，慢指针每次前进一步，快指针每次前进两步。在慢指针前进的过程中，同时修改其 next 指针，使得链表前半部分反序。最后比较中点两侧的链表是否相等。
    时间复杂度：O(n)
    空间复杂度：O(1)
    https://github.com/andavid/leetcode-java/blob/master/note/234/README.md在新窗口打开

链表代码

常见的链表操作

  • 单链表反转
  • 链表中环的检测
  • 两个有序的链表合并
  • 删除链表倒数第 n 个结点
  • 求链表的中间结点

数据结构 - 栈

3e20cca032c25168d3cc605fa7a53a0b.webp

todo

栈应用

  • 浏览器历史记录

数据结构 - 队列

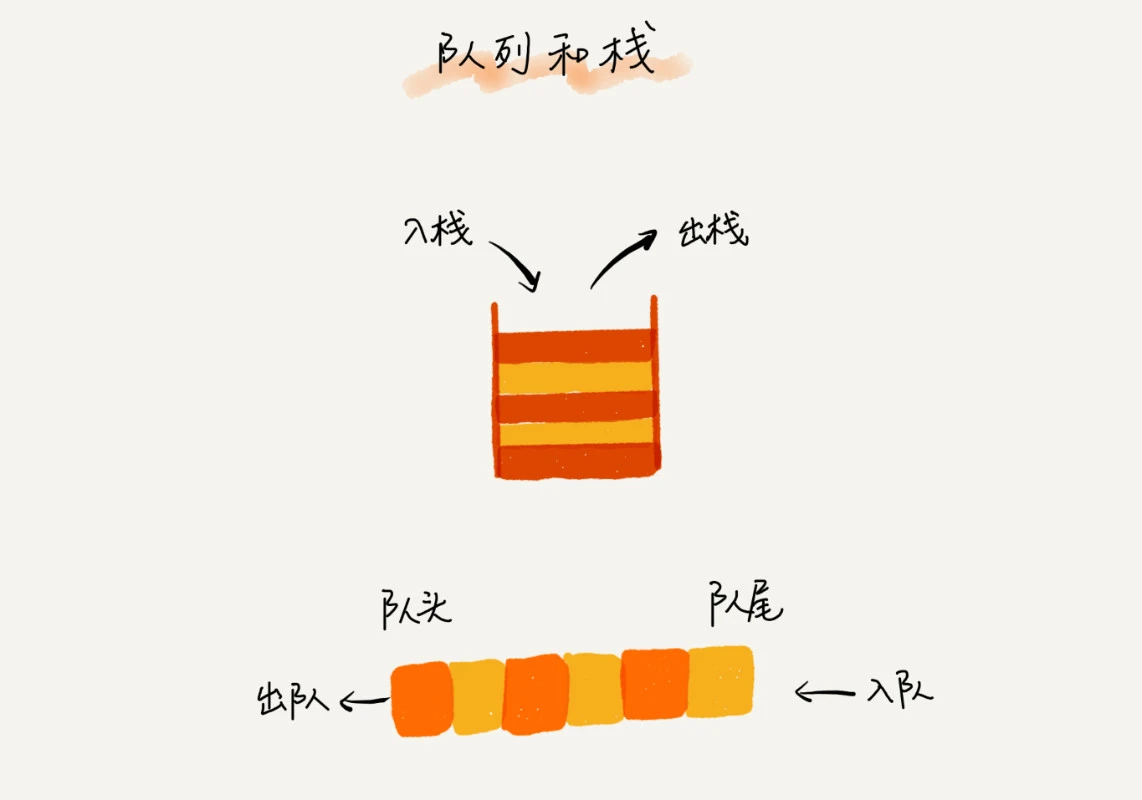
9eca53f9b557b1213c5d94b94e9dce3e.webp

todo

队列题目

  • 除了线程池这种池结构用到队列排队请求，还有那些场景用到队列排队请求？
  • 如何实现无锁并发队列
  • 表达式求值：中缀、后缀、逆波兰（RPN） https://www.nowcoder.com/practice/9566499a2e1546c0a257e885dfdbf30d在新窗口打开
    • 中缀转后缀
      • 数字直接写入RPN
      • 运算符优先级大进栈，优先级小先出栈写入RPN后进栈
      • "(" 进栈
      • ")" 出栈写入RPN
      • 遍历完成后，全部出栈，写入RPN
    • 后缀计算

实现方式 - 递归

一些算法/数据结构遍历需要用到的实现方法。

e.g.

int f(int n) {
  if (n == 1) return 1;
  return f(n-1) + 1;
}

什么时候用递归？

  1. 一个问题可以分为多个子问题
  2. 子问题解决方法类似
  3. 有中止条件

调试递归:

  1. 打印日志发现，递归值。
  2. 结合条件断点进行调试。

递归应用

  • DFS 深度优先搜索
  • 前中后序
  • 二叉树遍历

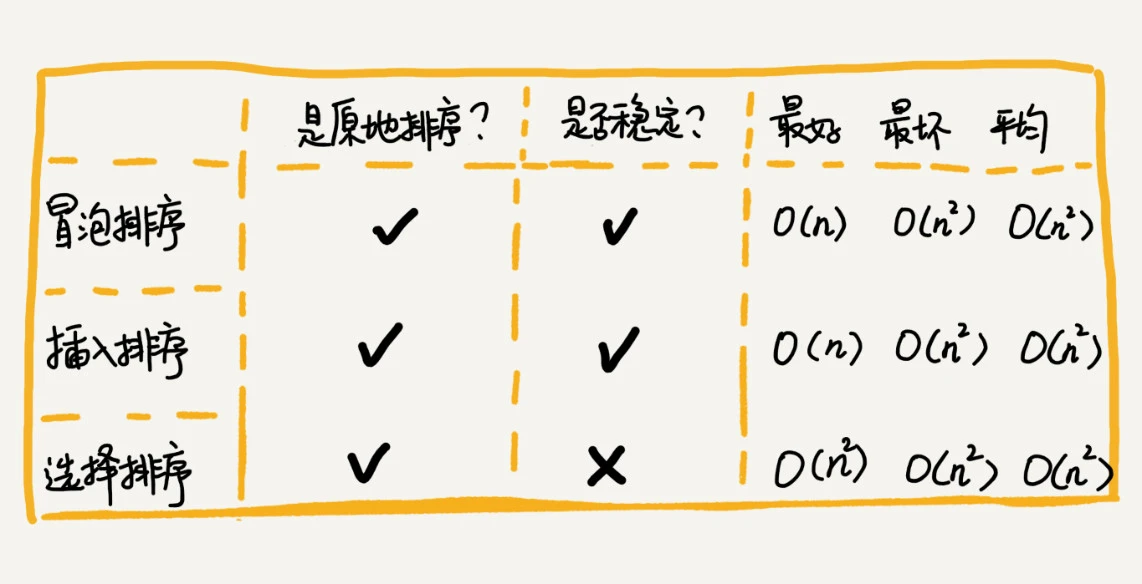
算法 - 排序🔥

排序算法时间复杂度： https://blog.csdn.net/LawssssCat/article/details/102798623在新窗口打开

常用的其实就三个：

  • 冒泡/插入 —— 习惯哪个用哪个
    • 冒泡 —— 数组、链表
    • 插入 —— 数组、双向链表
  • 归并 —— 数组，数据量大，同时内存够大
  • 快排 —— 数组，数据量中/大

冒泡排序（Bubble-Sort）

online visual demo: https://algorithm-visualizer.org/brute-force/bubble-sort在新窗口打开

具体的做法就是：从左往右把相邻的两个对比，把最大/最小的移到右边，然后缩小排序范围。

冒泡排序for数组
package org.example.algorithm;

/**
 * 冒泡排序
 */
public class SortBubble<T extends Comparable<T>> implements SortFunction<T> {
    @Override
    public void sort(T[] arr) {
        int n = arr.length;
        boolean swapped;
        do {
            swapped = false;
            for (int i = 1; i < n; i++) {
                if (arr[i].compareTo(arr[i - 1]) < 0) {
                    swapped = true;
                    T t = arr[i];
                    arr[i] = arr[i - 1];
                    arr[i - 1] = t;
                }
            }
            n--;
        } while (swapped);
    }
}

提示

冒泡排序写法有许多。上述的写法初看会有疑问 “为什么swapped为false就可以停止排序了？” 这里解释下：

有这疑问大概是不清楚这个代码做了什么，其实就三步：

  1. 检查排序是否正确（从小到大排序for i=1 .. if(arr[i-1] > arr[i])）
    • 如果排序不正确则需要进行下一步替换（swapped=true）
    • 如果排序正确，则任务完成(๑•̀ㅂ•́)و✧（swapped=false，while(swapped)不成立）
  2. 把最大的放最后，然后排除考虑
  3. 继续第一步（只是考虑范围变小了）

所以，“swapped为false就可以停止排序” 其实就是说 “排序正确！任务完成！”。很直白吧？

冒泡排序for链表
package org.example.algorithm;

/**
 * 冒泡排序 for 链表
 */
public class LinkedSortBubble<T extends Comparable<T>> implements LinkedSortFunction<T> {
    @Override
    public void sort(LinkedItem<T> head) {
        LinkedItem<T> cur = head;
        int n = count(head);
        boolean swapped;
        do {
            swapped = false;
            for(int i=1; i<n; i++) {
                LinkedItem<T> a = cur.getNext();
                LinkedItem<T> b = cur.getNext().getNext();
                if(a.getData().compareTo(b.getData())>0) {
                    { // 1. swap
                        cur.setNext(b);
                        a.setNext(b.getNext());
                        b.setNext(a);
                    }
                    swapped = true;
                }
                cur = cur.getNext(); // 2. next
            }
            n--;
            cur = head; // 3. reset
        } while(swapped);
    }

    public static void main(String[] args) {
        Integer[] arr = {2,5,9,3,7,6,0,1,99,22,44,4,8};
        LinkedItem<Integer> head = new LinkedBuilder<Integer>().build(arr);
        LinkedSortBubble<Integer> function = new LinkedSortBubble<>();
        function.show(head);
        function.sort(head);
        function.show(head); // [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 22, 44, 99]
    }
}

插入排序（Insertion-Sort）

online visual demo: https://algorithm-visualizer.org/brute-force/insertion-sort在新窗口打开

package org.example.algorithm;

/**
 * 插入排序
 */
public class SortInsertion<T extends Comparable<T>> implements SortFunction<T> {
    @Override
    public void sort(T[] arr) {
        for (int i = 1; i < arr.length; i++) {
            T value = arr[i];
            int j = i - 1;
            for (; j >= 0; j--) {
                if (value.compareTo(arr[j]) < 0) {
                    arr[j + 1] = arr[j];
                } else {
                    break;
                }
            }
            arr[j + 1] = value;
        }
    }
}

提示

插入排序的思想是先把左边的（已知的）排序好，再考虑新的值：

  1. 判断新的值位置是否正确（arr[j] > value）
    1. 如果新的值位置不对
      • 把左边已排序的后移，空出位置（arr[j+1] = arr[j]）
      • 再把新的值 “插入” 到对的位置上（arr[j+1] = value）
    2. 如果新的值位置对了
      • 继续第一步（只是考虑范围变大了）

💡插入排序这种逐渐把考虑范围扩大的做法和冒泡排序那种逐渐把考虑范围缩小的做法刚好相反！

选择排序（Selection-Sort）❌

警告

不建议使用

简而言之： 遍历多次，每次把最大/最小的放在前面/后面。

不建议使用的原因是它的最大、最小、平均时间复杂度都是O(n^2)，没有任何优化空间，属于最慢的排序算法。且不稳定。

好处是直观（一个对程序没啥用的好处）

348604caaf0a1b1d7fee0512822f0e50.webp

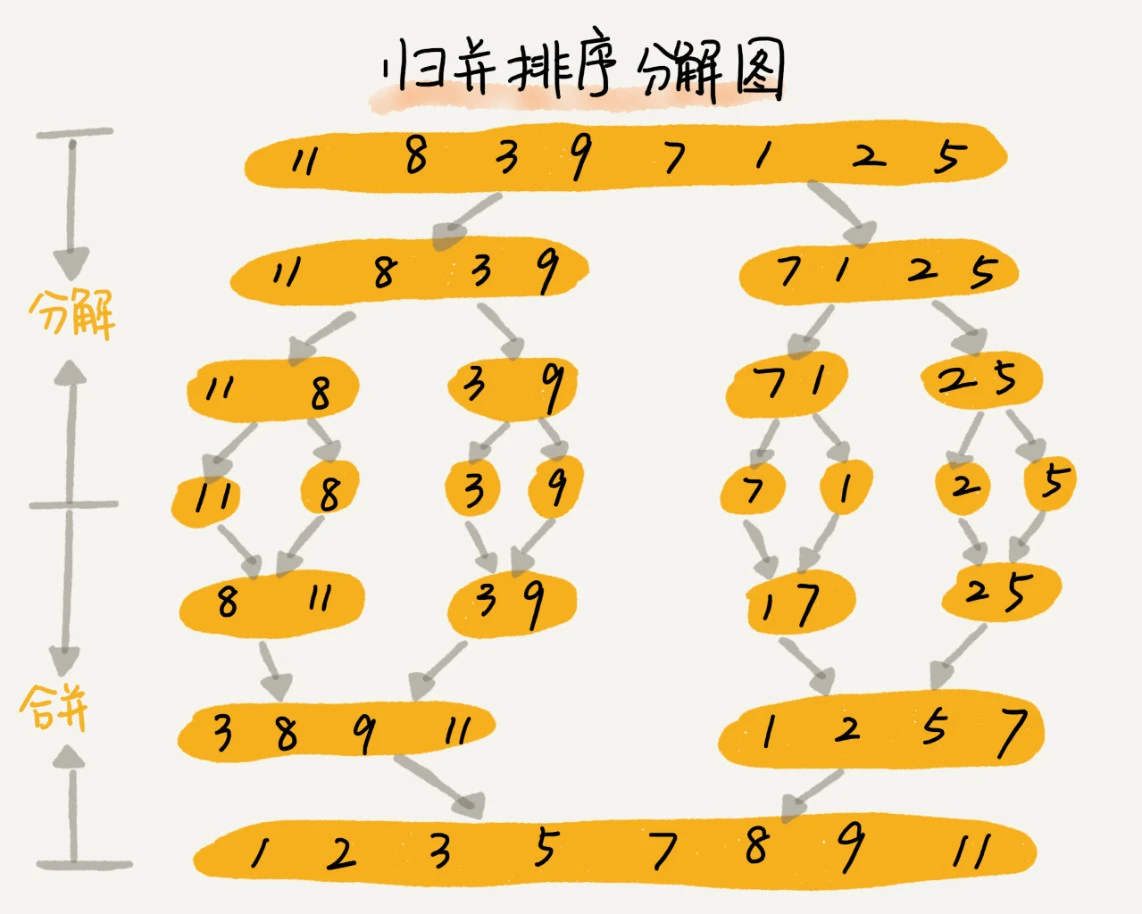
归并排序（Merge-Sort）✈️

Keywords: 分治、递归
online visual demo: https://algorithm-visualizer.org/divide-and-conquer/merge-sort在新窗口打开

提示

上述的三种排序（冒泡、插入、选择）时间复杂度高O(n^2)，适合小规模排序。下面介绍的归并排序、快速排序用了“分治”思想和“递归”实现，时间复杂度O(nlogn)，可以用在大规模排序上。

归并排序最好最坏平均备注
时间复杂度 O(nlogn)性能稳定！✅
空间复杂度 O(n)不是原地排序算法！❌
稳定性 稳定！✅

db7f892d3355ef74da9cd64aa926dc2b.webp

package org.example.algorithm;

/**
 * 归并排序
 * 递归、分治
 * 时间： O(nlogn)
 * 空间： O(n)
 * 稳定排序
 */
public class SortMerge<T extends Comparable<T>> implements SortFunction<T> {
    @Override
    public void sort(T[] arr) {
        if(arr.length<=1) {
            return;
        }
        T[] temp = (T[]) new Object[arr.length];
        _mergeSort(arr, temp, 0, arr.length);
    }
    void _mergeSort(T[] arr, T[] temp, int istart, int iend) {
        if(iend-istart>1) {
            int imid = (istart + iend) / 2;
            // divi
            _mergeSort(arr, temp, istart, imid);
            _mergeSort(arr, temp, imid, iend);
            // merge
            int it = istart;
            int il=istart, ir=imid;
            while(il<imid && ir<iend) {
                if(arr[il].compareTo(arr[ir])<0) {
                    temp[it] = arr[il];
                    il++;
                } else {
                    temp[it] = arr[ir];
                    ir++;
                }
                it++;
            }
            il = (il<imid) ? il : ir;
            imid = (il<imid) ? imid : iend;
            while(il < imid) {
                temp[it] = arr[il];
                il++;
                it++;
            }
            // copy
            while(istart<iend) {
                arr[istart] = temp[istart];
                istart++;
            }
        }
    }

    public static void main(String[] args) {
        Integer[] arr = {2,5,9,3,7,6,0,1,99,22,44,4,8};
        SortInsertion<Integer> function = new SortInsertion<>();
        function.show(arr);
        function.sort(arr);
        function.show(arr); // [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 22, 44, 99]
    }
}

快速排序（Quicksort）✈️

Alias: 快排
Keywords: 分治、递归
Rel: 二分查找（类似）
online visual demo: https://algorithm-visualizer.org/divide-and-conquer/quicksort在新窗口打开

提示

上述的“归并排序”和这里的“快速排序”都用到了“分治”思想。

归并排序最好最坏平均备注
时间复杂度O(n)O(n^2)O(nlogn)性能时好时坏 ☁️
空间复杂度 O(1)（不算递归开销） 原地排序算法！✅
稳定性 不稳定！❌

image.png

package org.example.algorithm;

/**
 * 快排 快速排序
 * 递归、分治
 * 时间：O(n)/O(nlogn)/O(n^2)
 * 空间：O(1)（不算递归开销）
 * 非稳定排序
 */
public class SortQuick<T extends Comparable<T>> implements SortFunction<T> {

    @Override
    public void sort(T[] arr) {
        _quickSort(arr, 0, arr.length-1);
    }

    private void _quickSort(T[] arr, int istart, int iend) {
        if(iend-istart>1) {
            int imid = _partition(arr, istart, iend);
            _quickSort(arr, istart, imid-1);
            _quickSort(arr, imid+1, iend);
        }
    }

    private int _partition(T[] arr, int il, int ir) {
        int iraw = ir;
        int index = il;
        T value = arr[iraw];
        for(int i=il; i<=ir; i++) {
            if(arr[i].compareTo(value)<0) { // swap -> i值往前放
                swap(arr, index, i);
                index++;
            }
        }
        swap(arr, index, iraw);
        // System.out.println(Arrays.toString(arr)); // debug usefully
        return index;
    }

    private void swap(T[] arr, int i, int j) {
        T temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }


    public static void main(String[] args) {
        Integer[] arr = {2,5,9,3,7,6,0,1,99,22,44,4,8};
        SortQuick<Integer> function = new SortQuick<>();
        function.show(arr);
        function.sort(arr);
        function.show(arr); // [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 22, 44, 99]
    }

}

堆排序

todo 大顶堆、小顶堆

线性排序 - 桶排序

todo https://time.geekbang.org/column/article/42038

线性排序 - 计数排序

todo https://time.geekbang.org/column/article/42038

线性排序 - 基数排序

todo https://time.geekbang.org/column/article/42038

算法 - 查找

Alias: 折半查找
Keywords: 分治、递归
online visual demo: https://algorithm-visualizer.org/divide-and-conquer/quicksort在新窗口打开

时间复杂度： O(logn)

注意

能使用二分查找的情况：

  1. 只针对数组（随机访问）数据类型。
  2. 有序！

局限：

  1. 数据量不能太小 —— 牛刀杀鸡
  2. 数据量不能太大 —— 底层数据不连续（但是，如果是抽象的数据空间呢？）
二分查找问题

  • 如何编程实现“求一个数的平方根”？要求精确到小数点后 6 位。

    提示

    在求一个数的平方根问题上，用二分查找并不是最优的。（只是这里讲到，所以提到）
    最优方法是用牛顿弦切法求解平方根，代码如下供大家参考：

    double number = 15; //待求平方根的数
double xini = 10;//初始点
while(xini*xini - number > 1e-6) {
  xini = (number + xini*xini)/2/xini;
}

  • 快速定位IP对应的省份地址

算法 - 回溯算法

回溯通常用递归实现。

解决问题：

深度搜索 DFS / 广度搜索 BFS

算法 - 贪心算法

如： 跳跃游戏（LeedCode 55）、分发饼干在新窗口打开

提示

贪心算法本质是先找每个阶段的 “局部最优”，从而推到 “全局最优”！

贪心和动态规划非常相似，属于 “有局部最优解” 的动态规划！

写贪心算法的核心是找到 “局部最优解”！但是，如何得知 “局部最优” 没有套路（因为需要数学证明）！
💡如果判断使用贪心算法？如果发现局部最优好像能推出全局最优，就试一下！至于数学如何证明，做题时不需要思考，样例通过了就行！

算法 - 动态规划

如： 最大背包问题、最大子序列在新窗口打开

提示

动态规划核心思想： “空间” 换 “时间” —— 通过避免重复计算来加速整体速度。

这个过程需要用到字典来保存中间计算结果，因此也称 “记忆化搜索”（recursion with memoization） / “带备忘录的递归”（memo） / “递归树的减枝”（Pruning）。

自低向上动态规划

动态规划求解步骤：

  1. 设计状态
  2. 确定状态转移方程
  3. 确定初始状态 （状态存到hash表，便于快速访问）
  4. 执行状态转移
  5. 计算最终的解

根据问题的维度可以划分为 “一维动态规划问题”、“二维动态规划问题”、... 一步步来。

问题：递推

如： 斐波那契数列在新窗口打开、青蛙跳台阶在新窗口打开

问题：编辑距离（Edit-Distance）

https://www.nowcoder.com/practice/3959837097c7413a961a135d7104c314在新窗口打开

对比两个字符串，可以对字符串编辑（添加/替换/删除）。求最小编辑次数。

参考： （按顺序，循序渐进，一个一个理解）

  1. LeetCode：718.最长重复子数组在新窗口打开
  2. LeetCode：1143.最长公共子序列在新窗口打开
  3. LeetCode：583.两个字符串的删除操作在新窗口打开
  4. LeetCode：72.编辑距离在新窗口打开

问题：背包问题

数据结构 - 跳表

Keywords: 二分查找
Ref: 红黑树（常用来对比）

用来查找的数据结构，查找的时间复杂度O(logn)

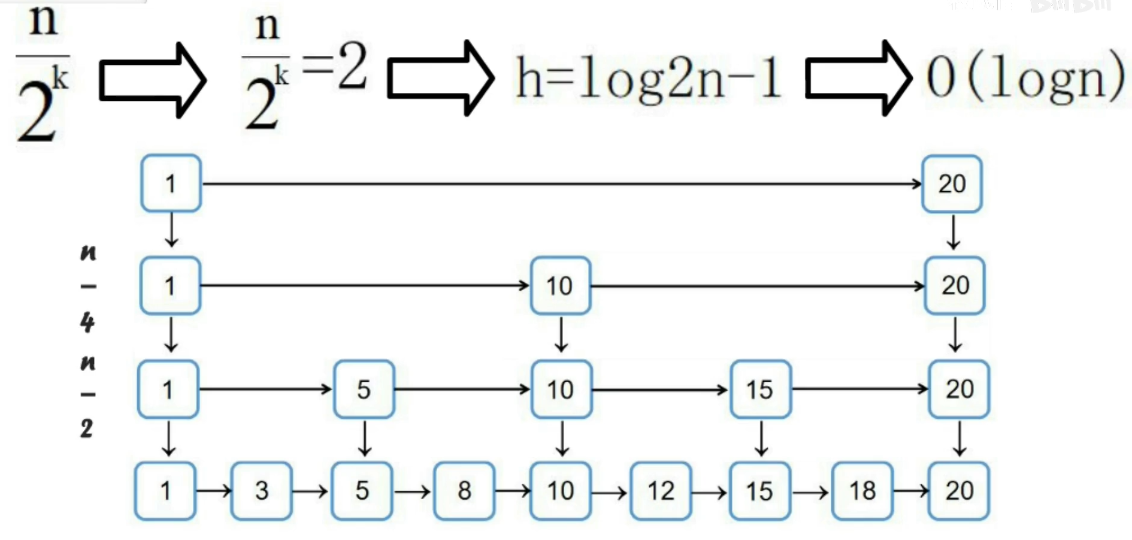
image.png

跳表问题

  • 为什么redis使用跳表来实现有序集合？而不是红黑树？

数据结构 - 树

todo

遍历

  • 深度优先
    • 先序、中序、后序
  • 广度优先
    • 队列

AVL树

参考：

每个节点中，左子节点和右子节点的高度差（平衡因子）不大于1。

插入/删除导致两边不平衡时，执行左旋/右旋/双旋操作，以平衡两边子树高度。

右旋： LL 1 （左边高，向右转）

左旋： RR 4（右边高，向左转）

左右双旋： LR 2

右左双旋： RL 3

红黑树

todo hashmap

高度差允许差1倍

问： java hashmap 为什么用红黑树，不用avl树

平衡二叉树平衡度调整频率使用场景
AVL树高高查询多，增/删少的场景
红黑树低低增/删频繁的场景

数据结构 - 堆

todo

数据结构 - 图

图的遍历有两种：深度优先/广度优先

定义： 邻接表在新窗口打开

遍历

图的遍历有两种策略

有递归/栈两种实现

参考